[BOJ 8907] 네온사인

PS가 뭔지 잘 모르거나 처음 접하는 사람에게 나는 이 문제를 소개 시켜 주고 싶다. 

 

https://www.acmicpc.net/problem/8907

8907번: 네온 사인

 

굉장히 좋은 문제이다. 주관적이긴 하지만 좋은 문제라 생각하는 이유들을 말해보겠다.

 

입출력 양식이 살짝 거슬리긴 하지만 잡설을 포함해도 4줄밖에 되지 않는 간략함과 직관으로 바로 이해할 수 있는 문제 상황이 좋은 문제가 되기 위한 첫 번째 조건을 만족한다.

 

두 번째 조건은 난이도이다. 당연히 너무 쉬운 문제는 별로이다. 풀어보면 단순한 문제 상황에 비해 생각만큼 쉽게 풀리지 않는 것을 알 수 있을 것이다. 하지만 너무 어려운 문제 또한 별로이다. 다행히 이 문제는 전혀 어렵지 않은 테크닉을 이용하여 해결한다. 이 문제를 PS 처음하는 사람들에게 소개 시켜 주고 싶은 이유 중 하나이다.

 

마지막으로 풀이가 멋있다. 단순하지만 생각하기 쉽지 않은 하나의 생각에서 출발하는 풀이를 보면 보통 탄식을 내뱉게 된다. 이 문제가 그랬다. 스스로 생각하지 못하고 다른 사람의 풀이를 보고 알게 되었었는데 머리를 한대 맞은 느낌이였었다.

 

 

한번 문제에 접근해보겠다.

가장 먼저 모든 삼각형을 직접 확인하며 세보는 풀이를 생각해볼 수 있다. 이 방법으로 해결된다면 별다른 고민 없이 구현하면 되기 때문이다. 아무 삼각형이나 잡고 단색 삼각형인지 확인 하는 것은 단순 구현의 범주이다. 구현만 나쁘지 않게 했다면 O(1)의 시간에 확인이 가능할 것이다. 이제 전체 삼각형의 개수에 대해 확인을 해야 되는데 O(n^3)개 정도의 삼각형이 있다는 것 또한 굉장히 자명한 사실이다. 이렇게 O(n^3)의 풀이가 완성된다.

 

이제 이 풀이로 문제를 해결할 수 있는지 확인 해보아야 한다. 문제에서 n의 최댓값은 1000으로 주어져있다. 보통 1초쯤의 시간을 위해서는 10^8개 정도의 연산이 가능하다고 보기 때문에 n^3의 풀이가 통과할지 살짝 불안불안하다. 테케의 개수 또한 주어져 있지 않아 굉장히 거슬리지만 어쩔 수 없다(이 문제의 가장 큰 흠이다).

 

귀찮은 구현이 아니므로 맞으면 장땡이라는 생각으로 제출을 해보았었다. 예상한 결과였지만 시간초과가 떴다. 다른 풀이가 필요한 것이다.

 

이렇게 하면 시간초과. 코드는 어떻게 삽입하지

 

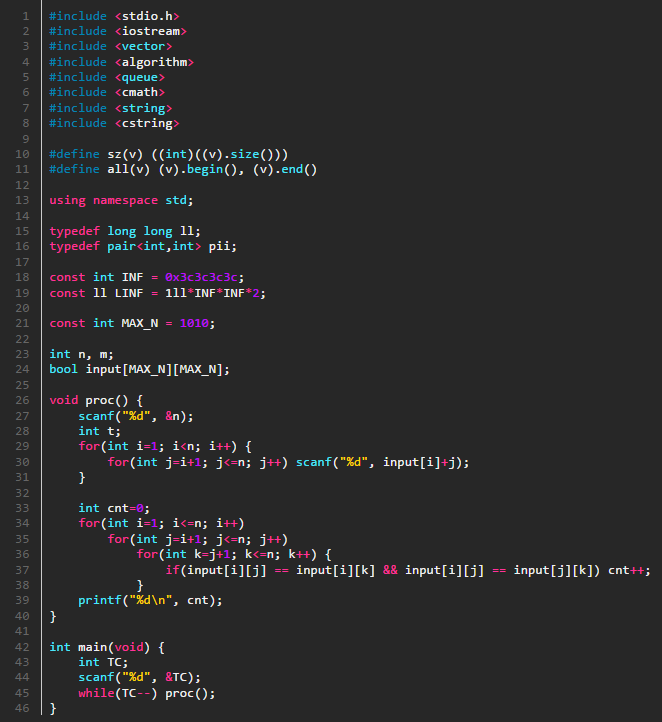
이 문제의 풀이의 핵심은 단색삼각형이 아닌 삼각형에 있다. 이색삼각형이라 부르겠다.

한점을 기준으로 두변의 색이 같아도 그 삼각형이 단색삼각형인지 확신 할 수 없다. 나머지 한 변을 한번 더 확인해봐야되고 여기서 나름의 시간이 소비 되는 것이다. 하지만 이색삼각형의 경우 얘기가 달라진다. 한 점을 기준으로 두 변의 색이 다르면(=이색각이라 하겠다) 해당 삼각형이 이색삼각형이라는 것을 확신할 수 있다.

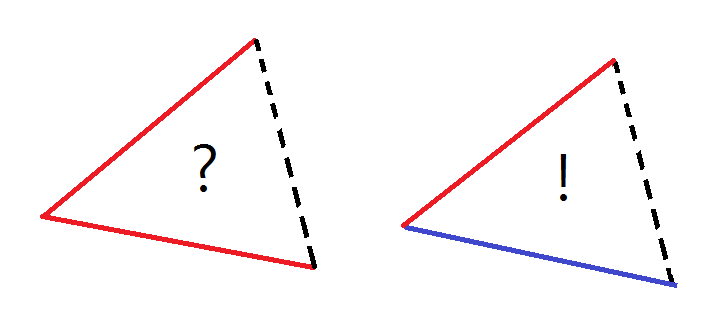
여기서 결정적인 성질이 하나 더 있는데 모든 이색삼각형은 이색각을 정확히 두개 포함한다는 것이다. 이 성질은 더블카운팅을 이용해 이색삼각형의 개수를 정확히 셀 수 있게 해준다. 모든 이색각은 이색삼각형을 생성하는데 한 이색삼각형마다 이색각이 두개 씩 있으므로 이색삼각형의 개수는 (이색각의 개수/2)가 되는 것이다.

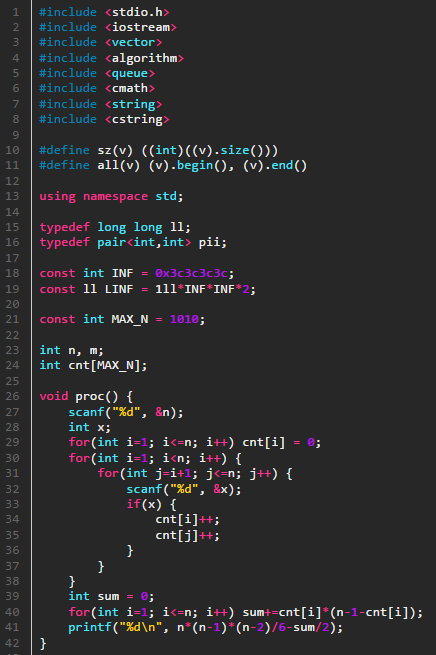
이색각의 개수는 각 점에 있는 빨간선과 파란선의 개수만 계산 할 수 있으므로 빠른 시간안에 이색삼각형의 개수를 구할 수 있고 전체 삼각형 개수에서 이색삼각형의 개수를 빼주면 단색삼각형이 개수가 나오는데 이 모든 과정은 O(n^2)의 시간에 해결할 수 있게 된다.

 

풀이